Robustness Metrics for Networked Structures
In collaboration with D. Towsley, S. Guha, A. Swami
Percolation theory predicts a phase transition in the global connectivity of a networked system when the probability of nodes/edges being present in the network passes a certain threshold. This approach has been extensively used in the literature to study the robustness of various networks to failiures. However, this approach has two main shortcommings:
- Precolation theory studies the infinite limit behavior in networks and there are limited studies that deal with small networks using percolation theory.
- General network connectivity is not robust enough for most of the technological and natural networks to ensure resilience to dynamics of the networks or failiures in network components. As an illustrative example, it is been observed that cellular networks need to have multiple pathways to maintain stability to perturbations during cellular metabolism. (Biconnectivity in Cellular Metabolism)
My Research Contribution
To address this shortcommings, I am developping and studying novel robustness metrics. Surprisingly, I have rigorousely proved that for bond/site percolation on the square lattice, the percolation threshold for Biconnectivity and Triconnectivity are the same as regular percolation threshold. Also, Newman et al. showed that the percolation threshold of biconnected components is similar to that of the regular percolation problem in configuration model networks.

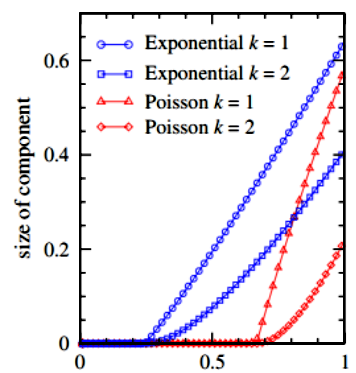
Universality Classes of Phase Transitions
The notion of universality classes roots from theory of phase transitions in physics. It is known that at the transition point in a continouos phase transition, the physical properties of the systems become scale-invariant. In addition, the corrlation length of system diverges at the transition point.
This gives rise to the concept of universality classes. The exponents of the sclae-free properties of the system at the transition point, define the universality class the system belongs to. The surprising fact about universality classes is that different physical systems observed that are governed by different microscopic structures often belong to the same universality class.
In my research, I am studying the type of the phase transitions and universality classes of the proposed robustness metrics.
This work has been presented in CompleNet 2018 and Distributed Analytics and Information Science International Technology Alliance and is in preparation for submission to Physical Review E.