Pattern Formation in Reaction-Diffusion Systems
In collaboration with D. Towsley and S.Guha
Turing Patterns in Reaction Difussion Systems
In his 1952 paper (The Chemical Basis of Morphogenesis), Alan Turing introduced the concept of Turing patterns. Since his nominal paper, scientists have broadened the scope of reaction diffusion systems that could result in Turing patterns. THese patterns appear in distinct natural phenomena ranging from vegetation patterns in deserts (vegetation patterns) to laser filamentation governed by nonlinear Schrodinger eqution (laser filamentation).
Laser Filamentation as a New Phase Transition
My research was motivated by this paper on laser filamentation. A extremely high power laser passes through a medium. This causes the medium to become plasma at some points in the space. The interaction of the high power laser and the plasma immitates the setting of a reaction diffusion system with different interacting entities.
The image below, shows the evolution of the intensity of the laser pulse as it travels in space. Each image is taken at a cross sextion of the laser beam at a certain distance from the source. The left most image is the nearest and the right most image is furthest one. Colors denote, the size of the connected clusters. Dark red colors denote larger components. As it can be seen from the image, at some point between image (h) and (i) the system looses its global connectivity.
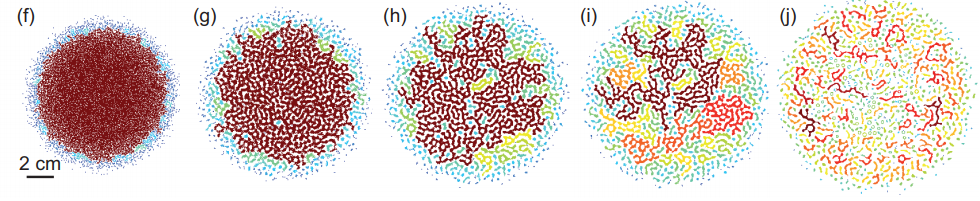
My Research Contribution
I developped a very simple single species reaction diffusion model with that mimics the phase transition behavior and percolation behavior of a wide variet of physical systems, one being the lase filamentation phenomena. The dynamics of the proposed model passes through various regimes of Turing patterns and is controllable by parameters in the model. The image below shows an snapshot of the system at the critical point.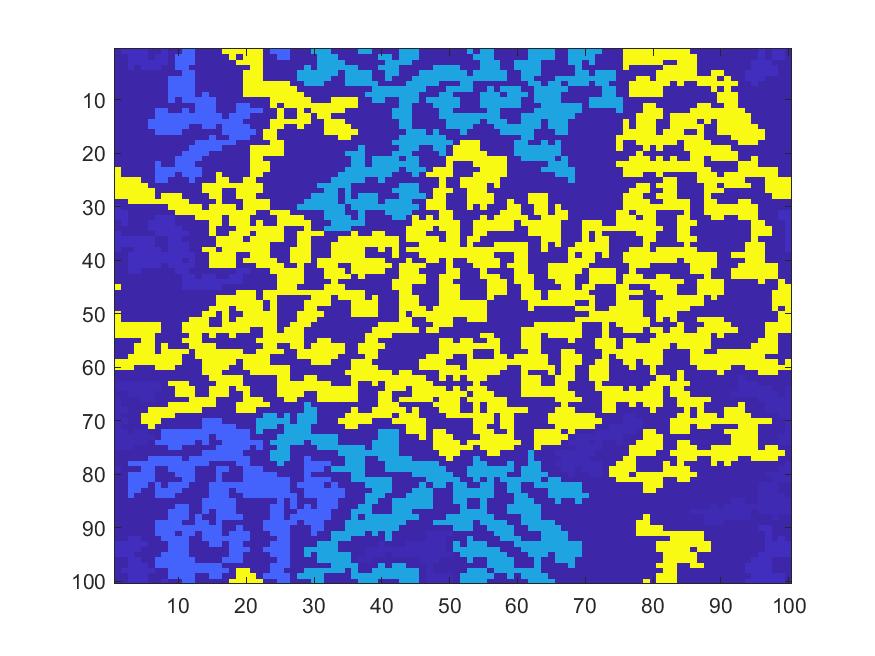
The Model
The proposed model is a very simple model in which the diffusion of particles in the system is dependant on the sum of the number of particles surrounding them. At time t, let n be the number of walkers on a lattice site and m the sum of the number of walkers on the neighboring sites. If n≥m the walker hops to one of the neighboring sites with equal probability and if n<m it does a lazy walk, i.e., hops only with probability exp(m-n). We declare a site active if there is at least one walker on it and inactive otherwise. Two neighboring sites have an edge if both are active. We compute the wrapping probability of the clusters formed at each time step, averaging over many simulations. We observe a sharp phase transition in the wrapping probability at a time threshold.This work has been presented in American Physical Society March Meeting 2018 in Spatiotemporal Pattern Formation session and is in preparation for submission to Physical Review E.